Z-ALTWSP Cont… Meets Z-WSPALT

Direction cosine and direction ratio of x y z axisПодробнее

Point Filters: Specify a single point by combining different coordinatesПодробнее

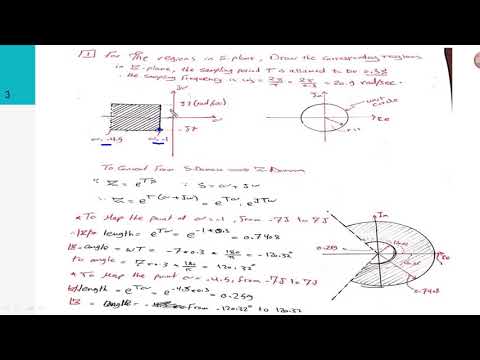
Mapping Between s plane and z planeПодробнее
Understanding the Z-TransformПодробнее

Different Sides of the MapПодробнее

Relationship of Laplace transform s-plane to Z-plane of the Z transform.Подробнее

Find the vector equation of the following planes whose Cartesian equations are `2x+3y-z-1=0`Подробнее

Angle between two lines| Angle between two lines whose direction cosines are given| 3D geometryПодробнее

Custom Solid (Calculus): Cross Sections Parallel to yAxis are Regular PentagonsПодробнее
#20 Direction cosine of the line y-x=0=z | How to find direction cosines and direction ratiosПодробнее

From Concept to Creation with the Xometry Add-In for SOLIDWORKSПодробнее

Projection of line segment on a given line|projection of line segment joining two points on a lineПодробнее

Direction CosinesПодробнее
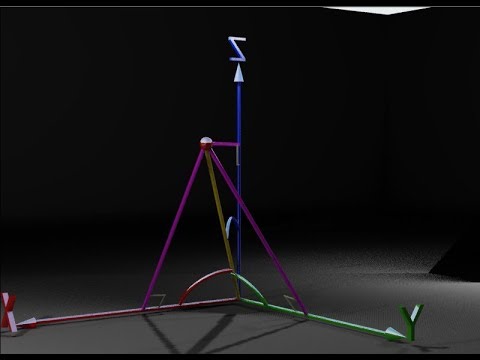
A line lies in XZ-plane and makes an angle `60^(@)` with Z-axis, find its inclination with X-axis.Подробнее

Understanding the Z-PlaneПодробнее

Custom Solid (Calculus): Cross Sections Parallel to yAxis are Isosceles RT's (Hypotenuse in Base)Подробнее